Interactive Online Tutorial Sheets
Tutorial Sheet Two Pin-Jointed Structures
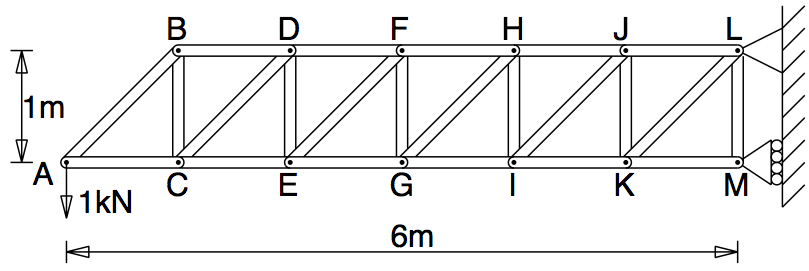
Q1: For the pin-jointed frame shown in figure Q1, find: the greatest compression load; the greatest tension load; the largest force in a diagonal member.
Note: Use T_{AB} in the maths formula to get $T_{AB}$. And all equations need to refer to the member you're trying to solve for. E.g. $T_{BC} = ...$
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ -1 + T_{AB}\sin45 = 0 $ $\therefore T_{AB} = \sqrt{2} $ |
|
| $ T_{AC} + T_{AB}\cos45 = 0 $ $\therefore T_{AC} = -1 $ |
|
| $ T_{BC} + T_{AB}\sin45 = 0 $ $\therefore T_{BC} = -1 $ |
|
| $ T_{BD} - T_{AB}\cos45 = 0 $ $\therefore T_{BD} = 1 $ |
|
| $ T_{BC} + T_{CD}\sin45 = 0 $ $\therefore T_{CD} = \sqrt{2} $ |
|
| $ -T_{AC} - T_{CE} - T_{CD}\cos45 = 0 $ $\therefore T_{CE} = -2 $ |
|
| $ T_{DE} + T_{CD}\sin45 = 0 $ $\therefore T_{DE} = -1 $ |
|
| $ T_{DF} - T_{BD} - T_{CD}\cos45 = 0 $ $\therefore T_{DF} = 2 $ |
|
| $ T_{DE} + T_{EF}\sin45 = 0 $ $\therefore T_{EF} = \sqrt{2} $ |
|
| $ - T_{CE} - T_{EG} - T_{CD}\cos45 = 0 $ $\therefore T_{EG} = -3 $ |
|
| $ T_{FG} + T_{EF}\sin45 = 0 $ $\therefore T_{FG} = \sqrt{2} $ |
|
| $ T_{FH} - T_{DF} - T_{EF}\cos45 = 0 $ $\therefore T_{FH} = 3 $ |
|
| $ T_{FG} + T_{GH}\sin45 = 0 $ $\therefore T_{GH} = \sqrt{2} $ |
|
| $ - T_{EG} I T_{GI} + T_{GH}\cos45 = 0 $ $\therefore T_{GI} = -4 $ |
|
| $ T_{HI} + T_{GH}\sin45 = 0 $ $\therefore T_{HI} = -1 $ |
|
| $ T_{HJ} - T_{FH} - T_{GH}\cos45 = 0 $ $\therefore T_{HJ} = 4 $ |
|
| $ T_{HI} + T_{IJ}\sin45 = 0 $ $\therefore T_{IJ} = \sqrt{2} $ |
|
| $ - T_{GI} - T_{IK} + T_{IJ}\cos45 = 0 $ $\therefore T_{IK} = -5 $ |
|
| $ T_{JK} + T_{IJ}\sin45 = 0 $ $\therefore T_{JK} = -1 $ |
|
| $T_{JL}$ | $ T_{JL} - T_{HJ} - T_{IJ}\cos45 = 0 $ $\therefore T_{JL} = 5 $ |
| $ T_{JK} + T_{KL}\sin45 = 0 $ $\therefore T_{KL} = \sqrt{2} $ |
|
| $ - T_{IK} - T_{KM} + T_{KL}\cos45 = 0 $ $\therefore T_{KM} = -5 $ |
|
| $ T_{KL} - P = 0 $ $\therefore P = 1 $ |
|
| $ Q $ | $ Q - T_{JL} - T_{KL}\cos45 = 0 $ $\therefore Q = 6 $ |
| $ T_{LM} = 0 $ | |
| $ -R - T_{KM} = 0 $ $\therefore R = 6 $ |
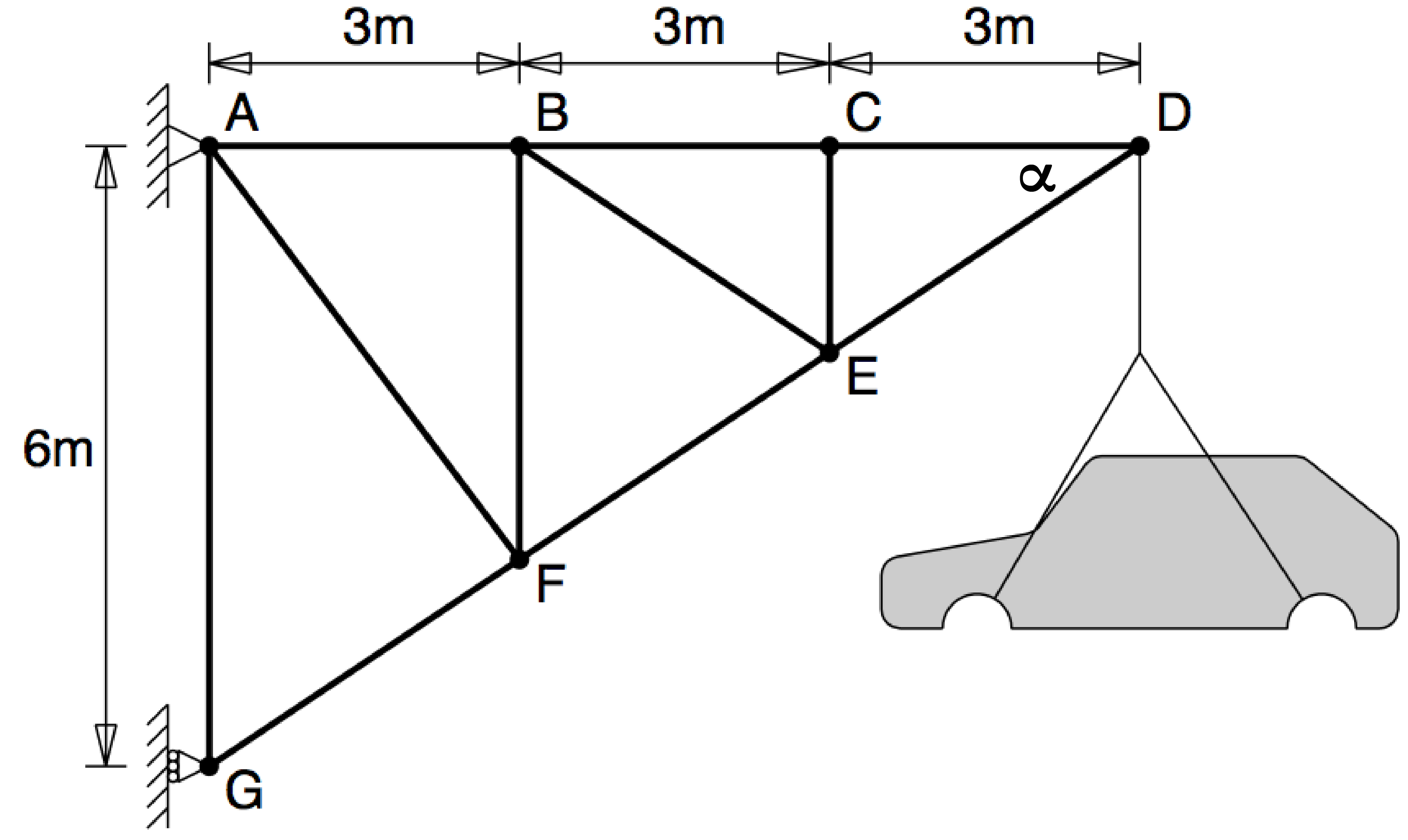
Q2: The framework shown in figure Q2 is used to support a steel car body of mass 200kg. Calculate the support reactions and the forces in members AB, BF and EF.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ T_{DE}\sin\alpha + W = 0 $ | |
| $ T_{DE}\cos\alpha + T_{CD} = 0 $ | |
| $ T_{DE} = \frac{-W}{\sin\alpha} = -1.80W = 3537N $ | |
| $ T_{CD} = − T_{DE}\cos\alpha = (\frac{3}{2})W = 2943N $ | |
| $ T_{BC} = T_{CD} = (\frac{3}{2})W = 2943N $ | |
| $ T_{CE} = 0 $ | |
| $ T_{BE} = 0 $ | |
| $ T_{EF} = T_{DE} = 3537 N $ | |
| $ T_{AB} = T_{BC} = (3/2)W = 2943N $ | |
| $ T_{BF} = 0 $ | |
| $ T_{AF} = 0 $ | |
| $ T_{FG} = T_{EF} = −W\sqrt{\frac{13}{2}} = 3537N $ | |
| $ R = T_{FG}\cos\alpha = (\frac{3}{2})W = 2943N $ | |
| $ T_{AG} = −T{FG}\sin\alpha = W = 1962N $ | |
| $ Q = T_{AB} = (\frac{3}{2})W = 2943N $ | |
| $ P = T_{AG} = W = 1962N $ | |
| $ P = W = 1962N $ | |
| $ Q=R =(\frac{3}{2})W = 2943N $ | |
| $ 6R = 9W $ |
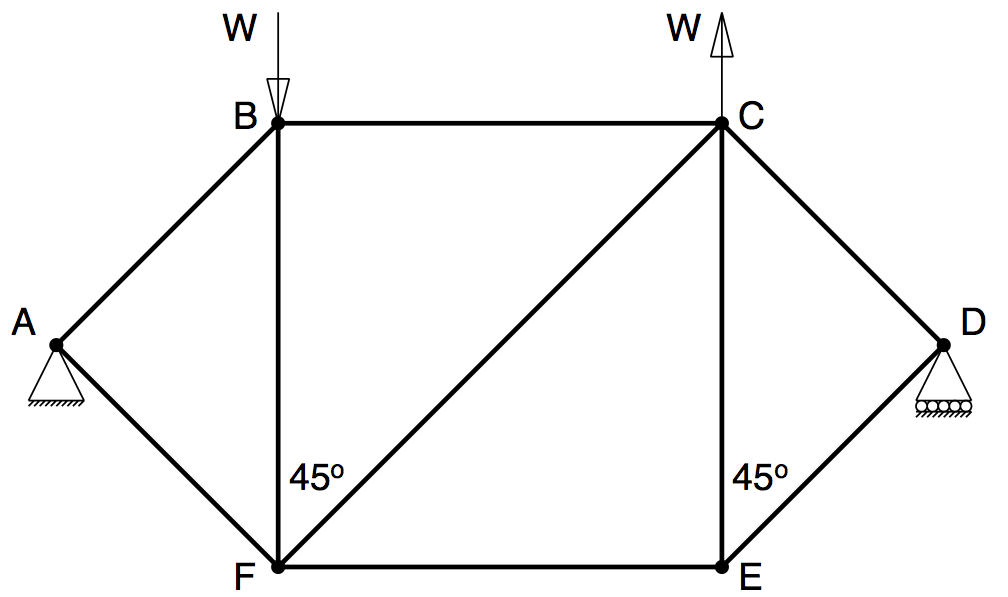
Q3: Find the support reactions and the forces in the framework shown in figure Q3. The three support reactions are P, Q and R.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ Q = 0 $ | |
| $ P - W + W - R = 0 $ | |
| $ W − 3W + 4R = 0 $ | |
| $ P = R = \frac{1}{2}W $ | |
| $ T_{AB} + P\cos45 = 0 $ $\therefore T_{AB}= -\frac{W}{2\sqrt{2}} $ |
|
| $ T_{AF} - P\sin45 = 0 $ $\therefore T_{AF}= \frac{W}{2\sqrt{2}} $ |
|
| $ W + T_{AB}\cos45 + T_{BF} = 0 $ $ T_{BF}=-\frac{3}{4}W $ |
|
| $ -T_{AB}\sin45 + T_{BC} = 0 $ $ T_{BC} = -\frac{W}{4} $ |
|
| $ T_{BF}+T_{AF}\cos45 + T_{CF}\cos45 = 0 $ $ T_{CF} = \frac{W}{\sqrt{2}} $ |
|
| $ -T_{AF}\sin45 + T_{CF}\sin45 + T_{EF} = 0 $ $ T_{EF} = -\frac{W}{4} $ |
|
| $ T_{DE}\sin45 - T_{EF} = 0 $ $ T_{DE} = -\frac{W}{2\sqrt{2}} $ |
|
| $ T_{CE} + T_{DE}\cos45 = 0 $ $ T_{CE} = \frac{W}{4} $ |
|
| $ T_{DE}\cos45 + T_{CD}\cos45 = 0 $ $ T_{CD} = \frac{W}{2\sqrt{2}} $ |
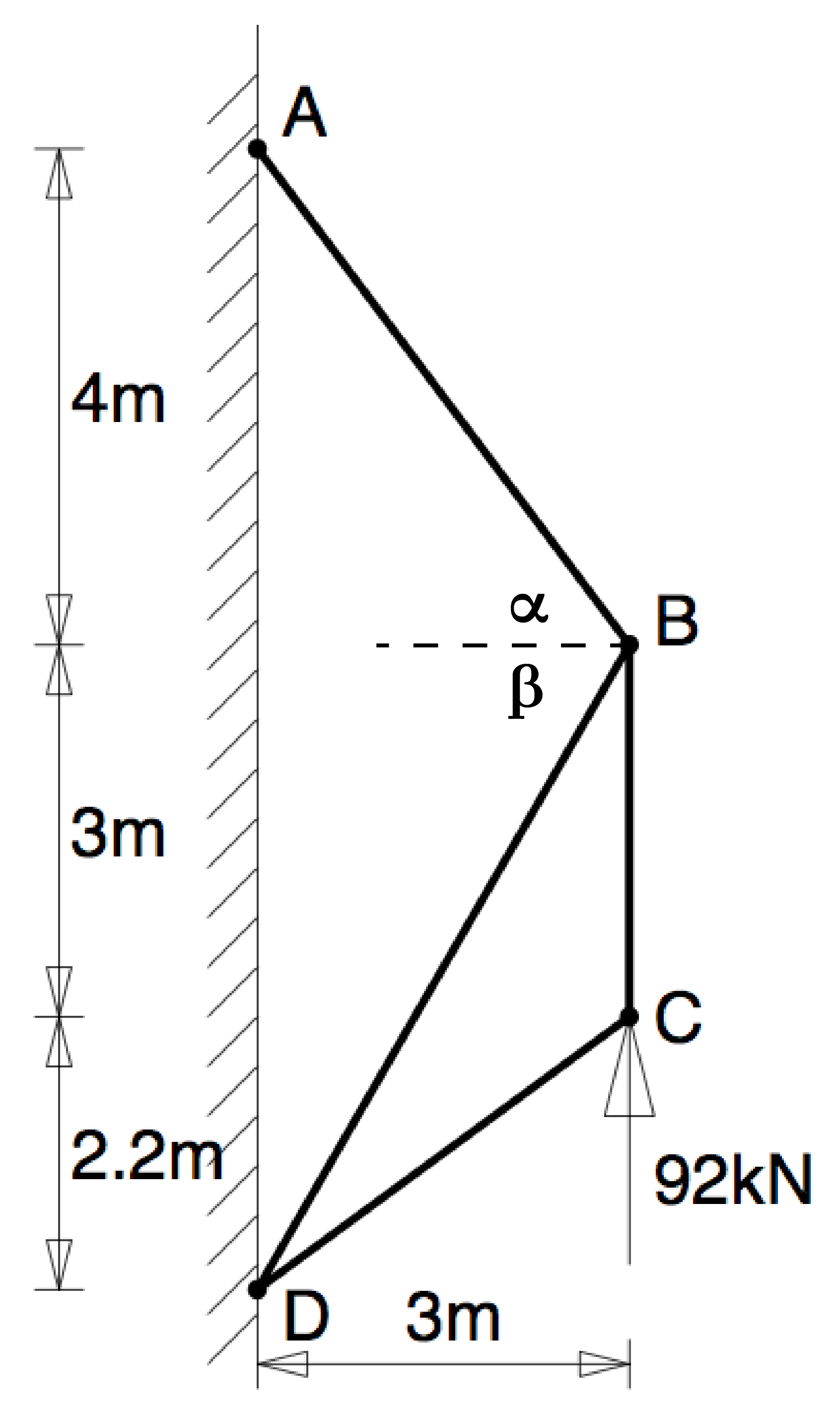
Q4: Find the internal forces in the pin-jointed structure shown in figure Q4.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ T_{AB}\cos\alpha + T_{BD}\cos\beta = 0 $ | |
| $ T_{AB}\sin\alpha + T_{BD}\sin\beta - T_{BC} = 0 $ | |
| $ \frac{3}{5}T_{AB} + \frac{3}{6}T_{BD} = 0 $ | |
| $ \frac{4}{5}T_{AB} + \frac{5.2}{6}T_{BD} = -92 $ | |
| $ T_{BD} = -\frac{6}{5}T_{AB} $ | |
| $ T_{AB} = -50 $ | |
| $ T_{BD} = 60 $ |
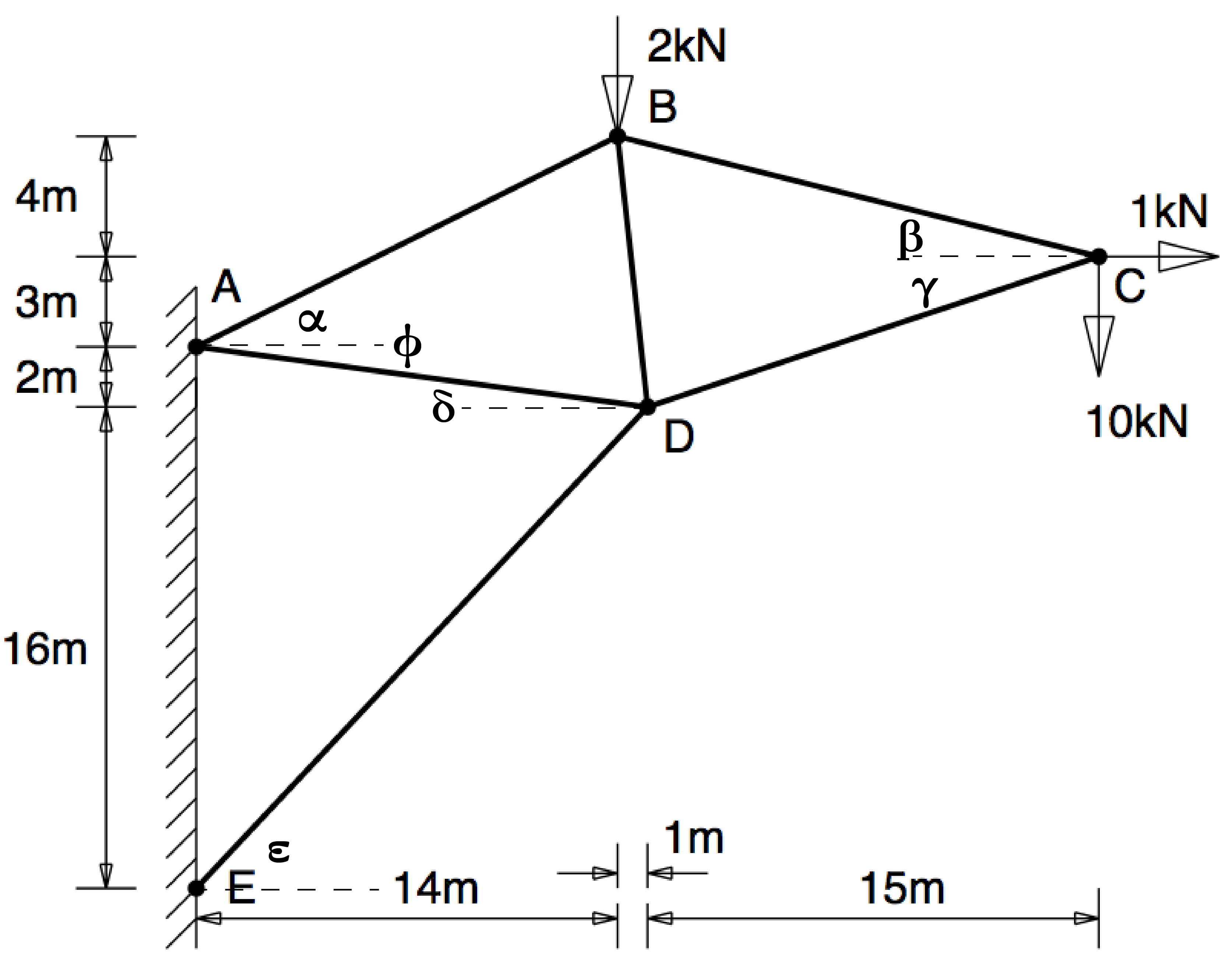
Q5: Find the internal forces in the pin-jointed structure shown in figure Q5
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ - T_{BC}\cos\beta - T_{CD}\cos\gamma + 1 = 0 $ | |
| $ T_{BC}\sin\beta - T_{CD}\sin\gamma - 10 = 0 $ | |
| $ -T_{AB}\cos\alpha + T_{BC}\cos\beta + T_{BD}\cos\delta = 0 $ | |
| $ -T_{AB}\sin\alpha - T_{BC}\sin\beta + T_{BD}\sin\delta - 2 = 0 $ | |
| $ -T_{AD}\cos\phi -T_{BD}\cos\delta - T_{DE}\cos\epsilon + T_{CD}\cos\gamma = 0 $ | |
| $ T_{AD}\sin\phi + T_{BD}\sin\delta - T_{DE}\sin\epsilon + T_{CD}\sin\gamma = 0 $ |
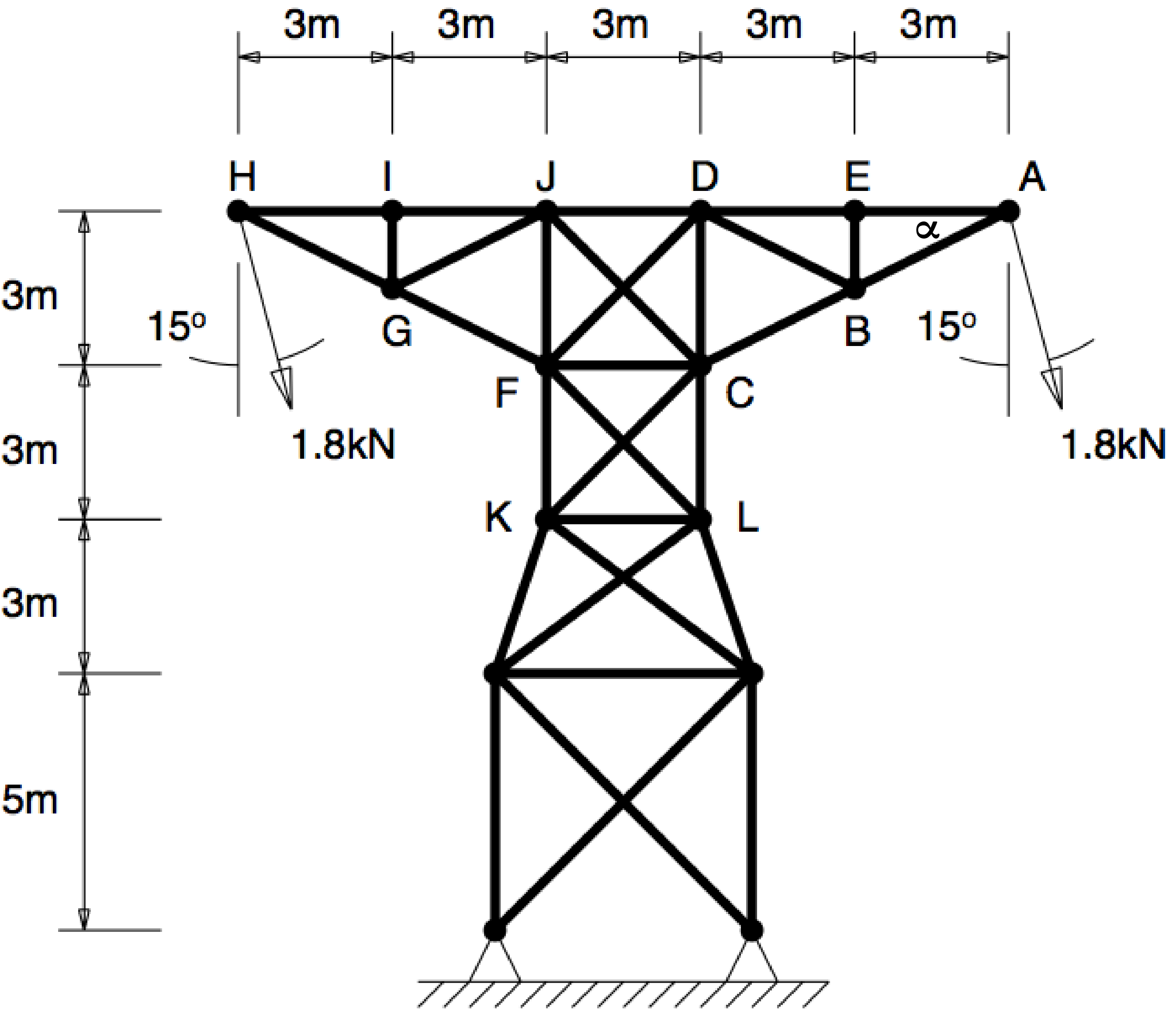
Q6: For the pylon structure shown in figure Q6, determine the forces in members AB, BD, BC and DE indicating whether each is in tension or compression.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ \alpha = 26.565 $ | |
| $ T_{AB}\sin\alpha + 1800\cos15 = 0 $ | |
| $ T_{AE} + T_{AB}\cos\alpha - 1800\sin15 = 0 $ | |
| $ T_{AE} = T_{DE} $ | |
| $ T_{BD} = 0 $ | |
| $ T_{BC} = T_{AB} $ |
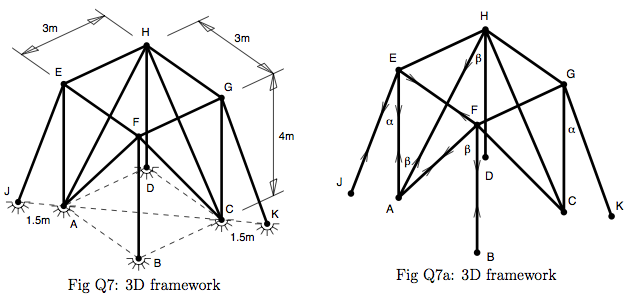
Figure Q7 shows a rectangular pin-jointed space frame. Guy wires EJ and GK are attached to the structure at E and G as shown and are tightened until the tension in each is 1800N. Find the force in each member of the structure.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ \alpha = \tan^{-1}(\frac{1.5}{4}) = 20.556 $ | |
| $ \beta = \tan^{-1}(\frac{3}{4}) = 36.870 $ | |
| $ T_{AE} = -T_{EJ}\cos\alpha = 1800\cos\alpha = -1685.4N $ | |
| $ T_{EF} = T_{EJ}\sin\alpha\cos45 = 1800\sin\alpha\cos45 = 446.91N $ | |
| $ T_{EF} + T_{AF}\sin\beta = 0 $ | |
| $ T_{AF} = -744.85N $ | |
| $ T_{AF} = T_{CF} $ due to symmetry | |
| $ T_{BF} = -T_{AF}\cos\beta - T_{CF}\cos\beta = -2T_{AF}\cos\beta = 1191.8N $ |