Interactive Online Tutorial Sheets

Tutorial Sheet Six Stress-Strain One

Q1: The stiffness of a spring (in its linear elastic range) is defined to be tension divided by extension. A metal bar under an axial load can be regarded as a spring. If its length is $L$, its cross-sectional area is $A$, and its Young’s modulus is $E$, show that its stiffness is $\frac{EA}{L}$.

Hints
$ F = \sigma A $
$x = \epsilon L$
$k = \frac{F}{x} $

Q2: The data in table 1 was obtained from a tensile test on a magnesium alloy specimen. The diameter of the specimen was 11.3 mm, and the extensions were measured over a gauge length of 50 mm. The extensiometer was set to zero when the specimen had been securely gripped in the jaws of the machine and the load reading was 2.5 kN. Plot (sketch) the stress-strain graph and hence obtain Young’s modulus and the 0.2% proof stress. At a stress of 250 MPa, what are: (a) the plastic strain, (b) the tangent modulus, and (c) the secant modulus.

Figure 1.1
Hints
Calculate the Cross-Sectional Area
$ \sigma = \frac{P}{A}, \epsilon = \frac{x}{L} $
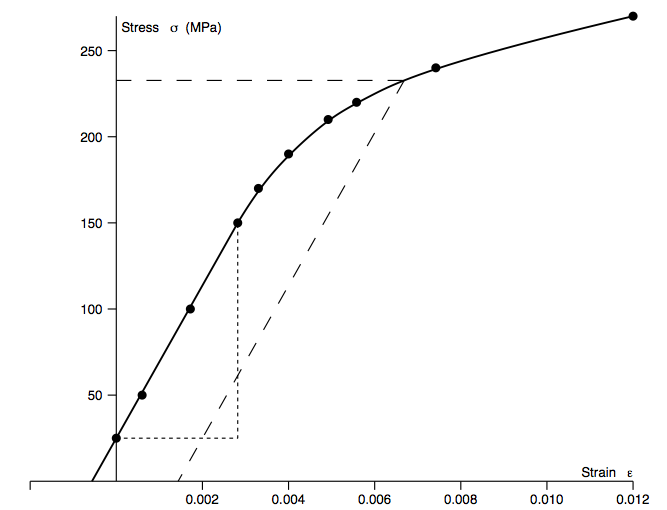Figure 1.1

Q3: An aluminium alloy rod of length 1.8 m and rectangular cross-sectional of area $ 250 mm^2 $ is subjected to a compressive load of 45 kN. Young’s modulus and Poisson’s ratio for the material are: $E = 71 GPa $ and $ ν = 0.33 $. Determine the decrease in length and increase in area of the bar.

Hints
$ \sigma_x = \frac{F}{A} $
$ \epsilon_x = \frac{\sigma_x}{E} $
$ \bigtriangleup A = (Y + \bigtriangleup Y)(Z + \bigtriangleup Z) - A $

Q4: A steel bar of length 2.5 m with a square cross-section of side 100 mm is subjected to an axial tensile load of 1300 kN. Assuming that for the steel, Young’s modulus E is 200 GPa, and Poisson’s ratio $v$ is 0.3, find the elongation of the bar and the change in cross-sectional area. [ Part of exam question in January, 2010 ]

Hints
Calculate Axial Stress, Strain and Extension
$ \bigtriangleup A = (Y + \bigtriangleup Y)(Z + \bigtriangleup Z) - A $
$ -2A(v\epsilon) $

Q5: A rod whose length is 0.5 m has a cross-sectional area which varies linearly from $400 mm^2$ at one end to $1000 mm^2$ at the other end. If Young’s modulus for the material is E = 140 GPa, calculate the increase in length of the bar when it carries a load of 160 kN.

Hints
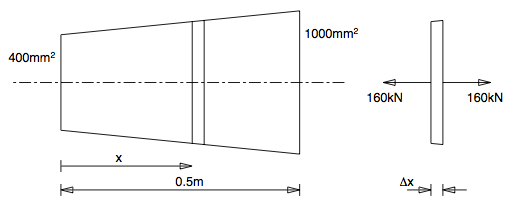Figure 1.1
$ A(x) = (400 + 1200x) \times 10^{-6}m^{2} $
$\frac{\bigtriangleup e}{\bigtriangleup x} = \epsilon = \frac{\sigma}{E} = \frac{P}{EA(x)}$, Integrate

Q6: Figure Q6 shows three circular rods of length 0.8 m: two are made of aluminium and have a diameter of 20 mm; the third is made of steel and has a diameter of 40 mm. The Young’s modulus of aluminium is 70 GPa and of steel is 210 GPa. The upper part of the figure shows the rods side-by-side and subjected to a compressive load of 100 kN. In the lower part, the rods are placed end-to-end and subject to the same compressive load. Find the contractions of each of the rods in each of the two loading cases.

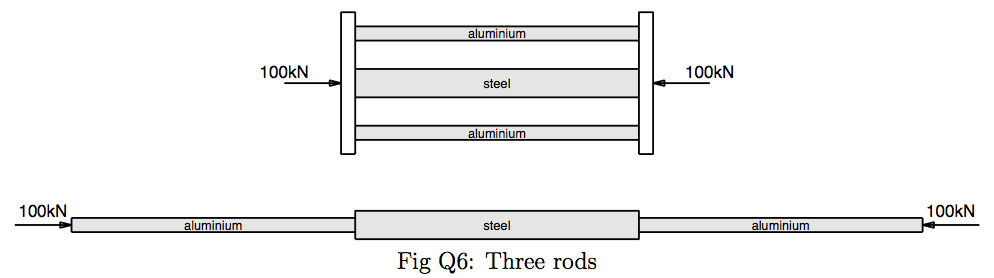
Figure 1.1
Hints
Calculate Cross-Sectional Areas
Case One: Load shared between rods hence common compression
Case Two: Common compressive force

Q7: A cube of material is subjected to a compressive stress σx in the x-direction. In the z- direction, there is no restraint, but, in the y-direction, there is a restraining compressive stress σy such that the strain in the y-direction is half that in the z-direction. Show that the strain in the x-direction is given by

$\epsilon_x = \frac{-\sigma_x}{E}\frac{(2-v)(1+v)}{2+v}$

[ Other part of exam question in January, 2010 ]

Hints
$\epsilon_x = \frac{\sigma_x}{E} - v\frac{\sigma_y}{E}$
$\epsilon_y = -v\frac{\sigma_x}{E} + \frac{\sigma_y}{E}$; $\epsilon_z = -v\frac{\sigma_x}{E} - v\frac{\sigma_y}{E}$
$-2v\sigma_x + 2\sigma_y = -v\sigma_x - v\sigma_y$

Q8: The stress-strain equation for a material (which does not obey Hooke’s law) may be approximated by the following equation (where the stress σ is given in Pascals).

$\epsilon = \frac{\sigma}{70\times10^9}+[\frac{\sigma}{2\times10^9}]^3$

Calculate the value of the 0.2% proof stress. What are the values of the tangent and secant modulus at a stress of 300 MPa.

Hints
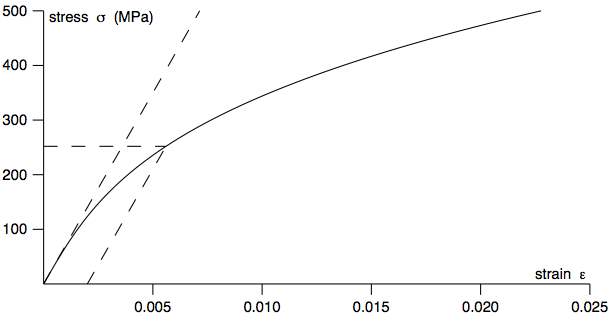Figure 1.1
Calculate $ \frac{d\epsilon}{d\sigma} $
$ \sigma = (\epsilon - s)A $