Interactive Online Tutorial Sheets
Tutorial Sheet One Equilibrium
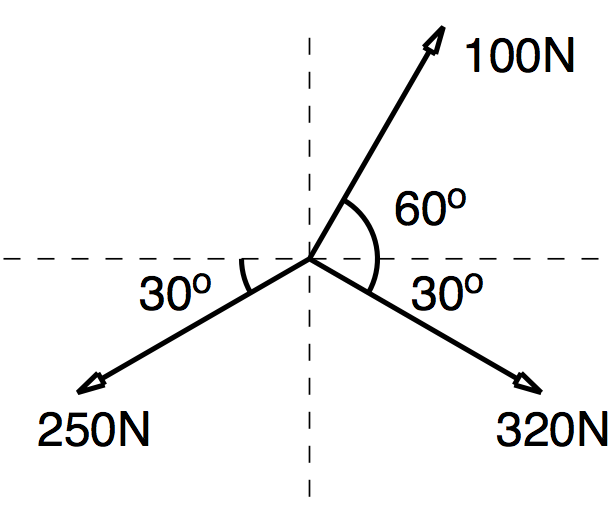
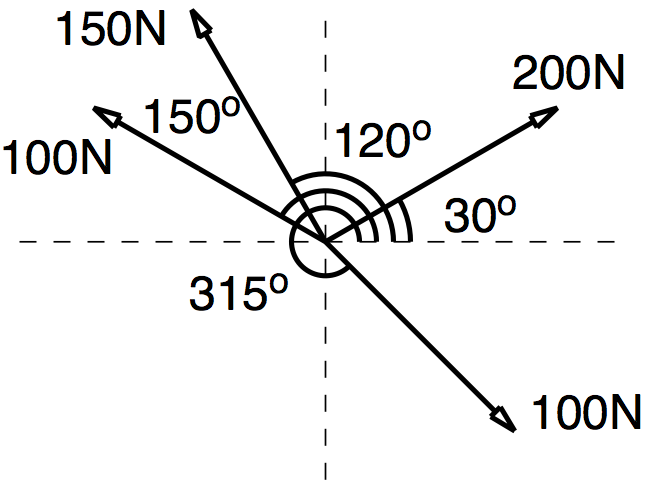
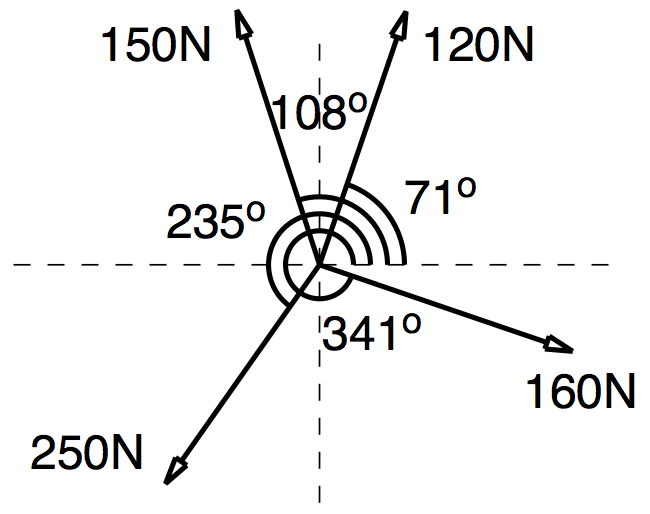
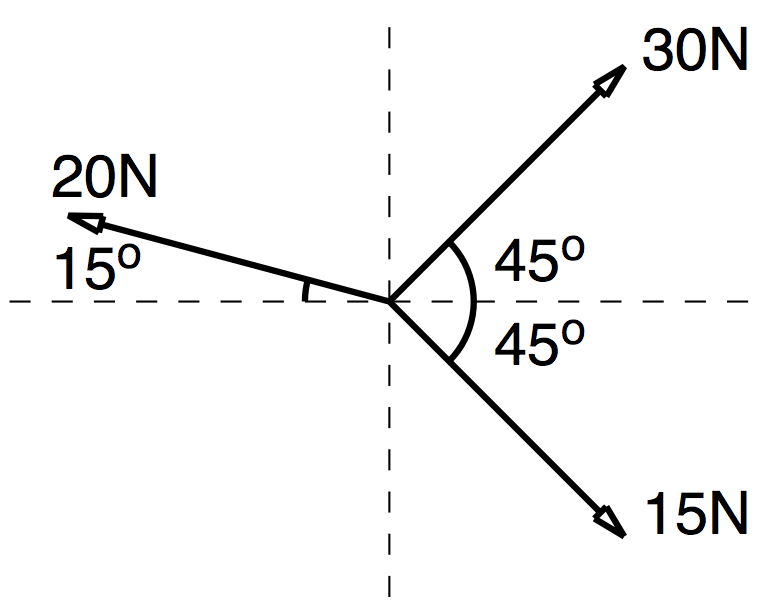
Q1: Determine the resultant of each system of concurrent forces shown in figures below. What force is needed to bring each system into a state of equilibrium?
Preview: $F = ma$
Click Here for Maths Help
$ 30\cos45 + 15\cos45 -20\cos15 = 12.501 $
$ 30\sin45 + 15\sin45 -20\sin15 = 15.783 $
$ \sqrt{(12.501^2+15.783^2)} = 20.134N $
$ \tan^-1(\frac{15.783}{12.501}) = 51.618 $
$ 100\cos60 + 320\cos30 - 250\cos15 = 110.622 $
$ 100\sin60 - 320\sin30 - 250\sin15 = 110.622 $
$ 227.153N $
$ -60.857 $
$ 200\cos30 + 150\cos120 + 100\cos150 + 100\cos315 = 82.313 $
$ 200\sin30 + 150\sin120 + 100\sin150 + 100\sin315 = 209.193 $
$ 224.804N $
$ 68.521 $
$ 120\cos71 + 150\cos108 + 250\cos235 + 160\cos341 = 0.604 $
$ 120\sin71 + 150\sin108 + 250\sin235 + 160\sin341 = −0.758 $
$ 0$
$ 0 $
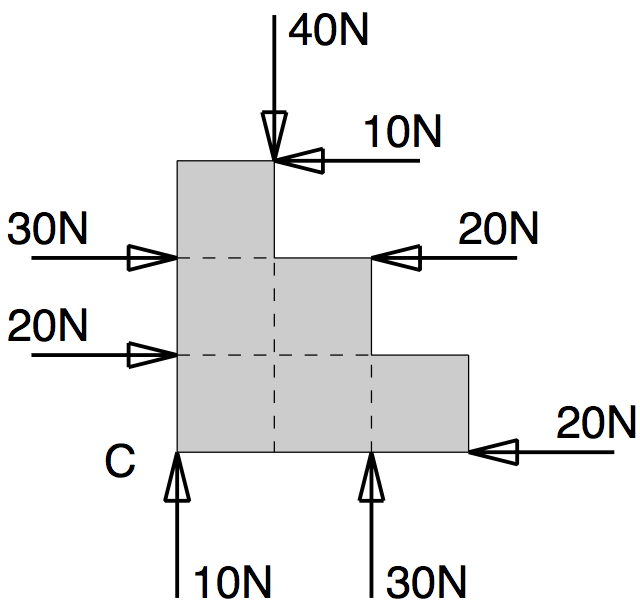
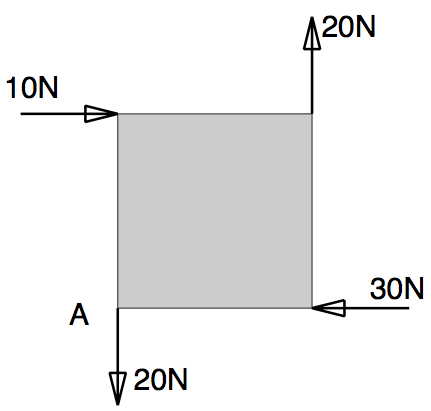
Q2: The shaded shapes in figure Q2 are made up of squares of side a = 50mm. Find the resultant force and/or couple of each system of planar forces.
Preview: $F = ma$
Click Here for Maths Help
$ 10 - 30 = -20 $
$ 20 - 20 = 0 $
$ -10a + 20a = 10a $
$ 18 - 29 + 82\cos45 = 47 $
$ 82\sin45 - 11 = 47 $
$ 36a + 11a = 47a $
$ 47\sqrt{2} = 66.5N $
$ 45 degrees $
$ 30 + 20 - 10 - 20 - 30 = 0 $
$ 10 + 30 - 40 = 0 $
$ 20a + 30(2a) + 40a -10(3a) - 20(2a) - 30(2a) = -10a $
$ 10a = 0.5Nm $
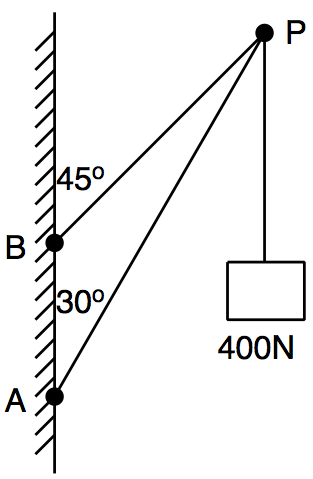
Q3: Figure Q3 shows a 400N load supported by a combination of a straight strut AP and a cable BP. Find the forces in the strut and the cable.
Preview: $F = ma$
Click Here for Maths Help
$ T_{AP}\sin30 + T_{BP}\sin45 = 0 $
$ 400 + T_{AP}\cos30 + T_{BP}\cos45 = 0 $
$ T_{AP} = \frac{-400}{(cos30-sin30)} = -1092.8N $
$ T_{BP} = \frac{T_{AP}\sin30}{\sin45} = 772.7N $
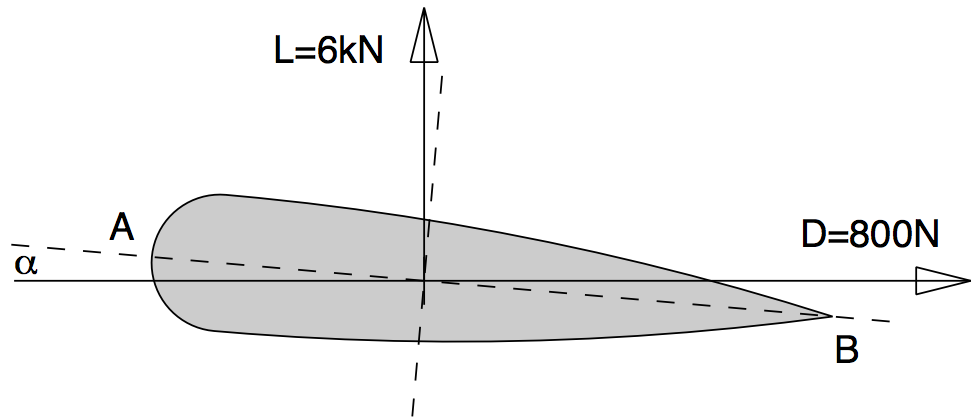
Q4: In level flight, the chord AB of an aeroplane wing makes an angle $ \alpha = 5^\circ $ with the horizontal as in figure Q4. The resultant effect of the wind pressure on the wing for such conditions is defined by the load L and drag D components as shown. Resolve these forces into components parallel and perpendicular to the chord AB. Find also the resultant of the lift and drag components.
Preview: $F = ma$
Click Here for Maths Help
$ D\cos\alpha−L\sin\alpha = 800\cos5 − 6000\sin5 = 274.0N $
$ D\sin\alpha + L\cos\alpha = 800\sin5 + 6000\cos5 = 6046.9N $
$ \sqrt{(L^2+D^2)} = \sqrt{(6000^2+800^2)} = 6053.1N $
$ \tan^{−1}(\frac{L}{D}) = \tan^{−1}7.5 = 82.41 $
Q5: Figure Q5 shows a steel shaft comprising a cylinder of length 1m and diameter 60mm to which are attached two discs as shown. The shaft is supported at its ends by two bearings. Sketch the free body diagram of the shaft and estimate the reaction forces at the bearings.
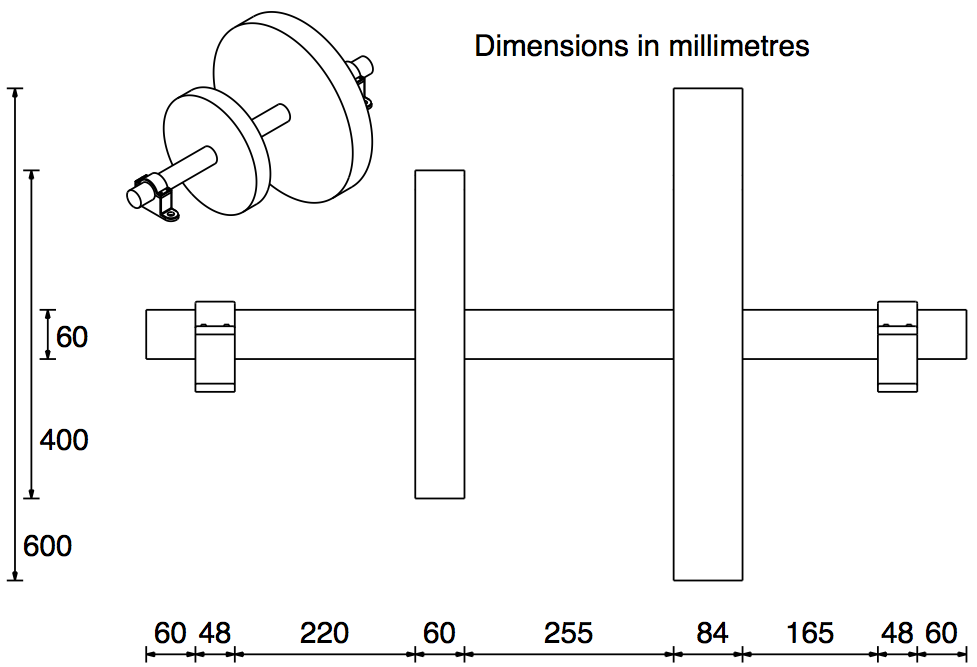
Preview: $F = ma$
Click Here for Maths Help
$ \rho\pi(0.03)^2\times1 = \rho\pi(0.9\times10^{-3}) $
$ \rho\pi(0.2^2 - 0.03^2)\times0.06 = \rho\pi(2.346\times10^{-3}) $
$ \rho\pi(0.3^2 - 0.03^2)\times0.084 = \rho\pi(7.484\times10^{-3}) $
$ R_1 + R_2 = m_1 + m_2 + m_0 = \rho\pi(10.730\times10^{-3}) $
$ 0.832R_2 = 0.274m_1g + 0.416m_0g + 0.601m_2g = (5.515\times10^{−3})\rho\pi g $
$ 0.832R_1 = 0.558m_1g + 0.416m_0g + 0.231m_2g = (3.412\times10^{−3})\rho\pi g $
$ (6.629\times10^{−3})\rho\pi g = 1604 N $
$ (4.101\times10^{-3})\rho\pi g = 992 N $
Q4: Figure Q6 shows a typical design for a vehicle weighbridge. Each of the levers has a : b in the ratio 1 : 10 as shown. A balance load of W = 12N is required on the lowest lever. Assuming that the centre of mass of the vehicle is midway between its axles and that the vehicle is symmetrically placed on the weighbridge, find the mass of the vehicle. What happens if the assumptions are not valid?
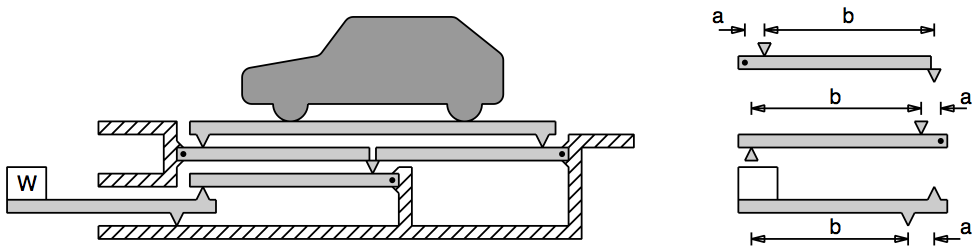
Preview: $F = ma$
Click Here for Maths Help
$ A = 10W = 120 $
$ B = 11A = 1320 $
$ B = B_1 + B_2 $
$ Mg = C_1 + C_2 = 11(B_1 + B_2) = 11B = 14520 $
$ \frac{14520}{9.81} = 1480kg $
Q7: For the crane jib shown in figure Q7, find the forces in members AB and AC; the tension in the cable DE; the reaction components at hinge H; and the supporting forces (including any moments) required on the shaft S.
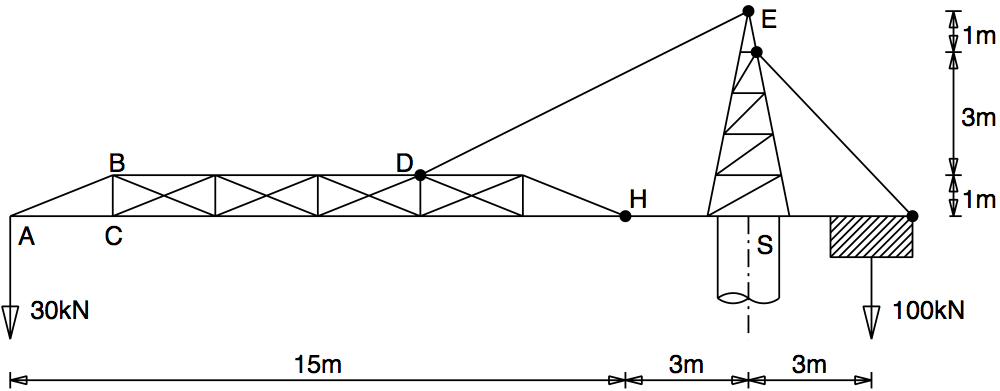
Preview: $F = ma$
Click Here for Maths Help
$ T_{AC} + T_{AB}\cos\alpha = 0 $
$ 30 - T_{AB}\sin\alpha = 0 $
$ \frac{30}{\sin\alpha} = 80.78kN $
$ -80.78\times\frac{2.5}{\sqrt{7.25}} = -75kN $
$ R_1 - T_{DE}\cos\beta = 0 $
$ R_2 + T_{DE}\sin\beta - 30 = 0 $
$ \frac{30\times15\times\sqrt{80}}{4\times7} = 143.75kN $
$ 128.57kN $
$ -34.29kN $
$ S = 130kN $
$ M_{S} = 30 \times 18 - 100 \times 3 = 240kNm $
Q8: A long ladder leans against a wall at an angle of $ 30^\circ $ to the vertical as shown in figure Q8. The wall is assumed smooth and the coefficient of friction between the ladder and the ground is 0.55. A builder climbs the ladder. Sketch the free body diagram for the ladder. What is the frictional force at the base when the builder is half-way up? How far can the builder go up the ladder before disaster strikes? If you were told that the coefficient of friction is in fact 0.6, would you climb the ladder to the top?
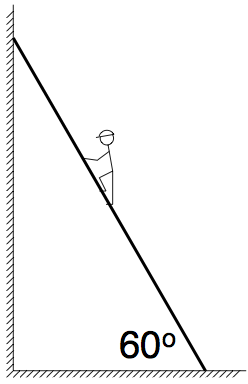
Preview: $F = ma$
Click Here for Maths Help
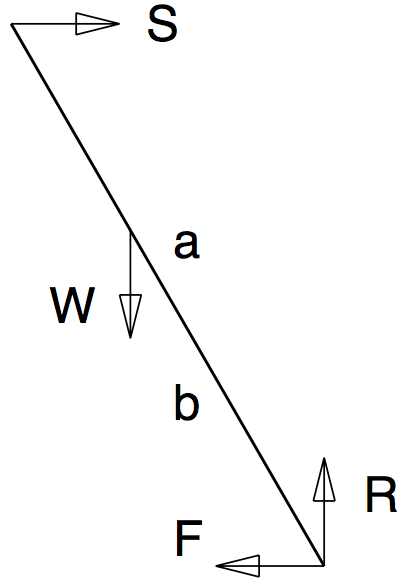
$ S = F $
$ W = R $
$ (a \cos 30)S = (b \sin 30)W $
$ F = S = \frac{b}{a}W(\tan30) = \frac{b}{a}R(\tan30) $
$ b = \frac{a}{2} $
$ F = 0.2887W = 0.2887R $
$ \frac{b}{a} = \frac{0.55}{\tan30} = 0.9526 $
$ \frac{F}{R} = \tan30 = 0.5774 $