Interactive Online Tutorial Sheets
Tutorial Sheet Four Newton's Laws, Friction, Non-Constant Acceleration
Q1: A crane is lifting a crate of mass 20kg with an upward acceleration of $2ms^{-2}$ by means of a single cable. What is the tension ($T$) in the cable?
\ddot{x} => $ \ddot{x} $
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ T - mg = m\ddot{x} $ | |
| $ T = m\ddot{x} + mg $ | |
| $ T = 316N $ |
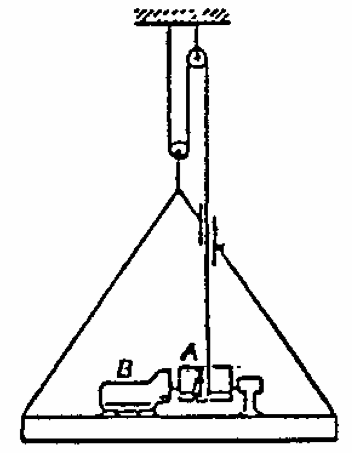
Q2: The platform, together with the load it carries, weighs 3000N, and is raised by winding the supporting cable around the drum A which is driven by the motor and gear unit B so as to give tension of 1200N in the cable. Find the initial acceleration of the platform. What is the initial acceleration of the part of the cable between the drum and the upper pulley?
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ 3T - mg = m\ddot{x} $ | |
| $ x = 1.96ms^{-1} $ |
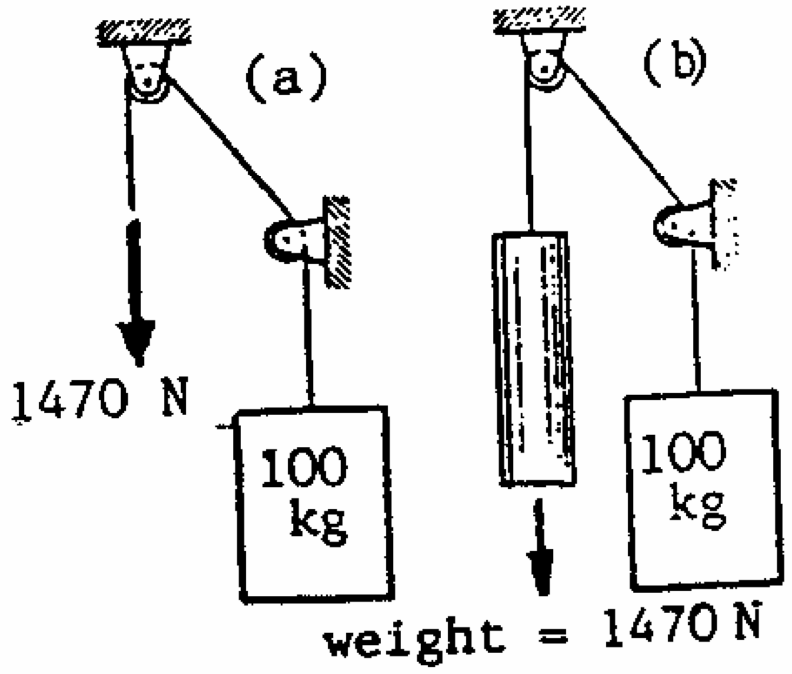
Q3: Determine the acceleration of the 100kg mass for each of the cases illustrated. The mass and friction of the pulleys are negligible. Hint - Take care to draw accurate Free Body Diagrams.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ T - mg = m\ddot{x} $ | |
| $ T = 1470N $ | |
| $ \ddot{x} = 4.89ms^{-2} $ | |
| $ T - mg = m\ddot{x} $ | |
| $ Mg - T = M\ddot{x} $ | |
| $ Mg - mg = \ddot{x}(M+m) $ | |
| $ \ddot{x} = 1.96ms^{-2} $ |
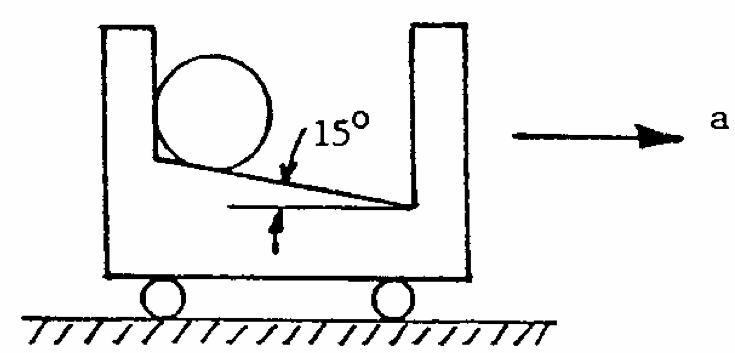
Q4: The frame shown is given a steady horizontal acceleration a = 2g. Determine the reaction between the sphere, which weighs 10N, and the vertical surface.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ R\cos15 - mg = m\ddot{y} = 0 $ | |
| $ F + R\sin15 = m\ddot{X} = 2gm = 2 \times 9.81 \times m $ | |
| $ F + mg\tan15 = 2mg $ | |
| $ F = mg(2 +\tan15) = 17.32N $ |
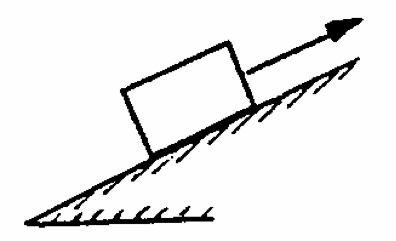
Q5: The crate shown has a mass of 15kg and is being pulled up a plane at 30 degrees by a chord parallel to the plane. Calculate the tension necessary to give the crate an acceleration parallel to the plane of $5ms^{-2}$. The coefficient of friction is 0.3.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ F = \mu R $ | |
| $ mg\cos30 - R = m\ddot{y} = 0 $ | |
| $ T - F - mg\sin30 = m\ddot{x} = 5m $ | |
| $ T - \mu R -mg\sin30 = 5m $ | |
| $ T - \mu (mg\cos30) - mg\sin30 = 5m $ |
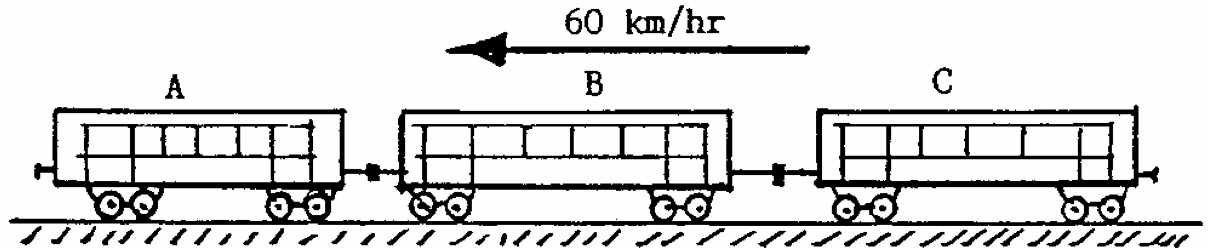
Q6: The electric train shown consists of three coaches A,B,C of mass 35t, 45t and 35t respectively. It is travelling at $60kmh^{-1}$ when the brakes are applied to coaches A and B, giving a braking force on each of these coaches of 25kN, but no braking force on C. Calculate the force in each coupling.
Note: Coupling A-B = $ T $ &: B-C = $ N $.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ 115 $ tonnes | |
| $ \frac{F}{M} = a = \frac{50}{115} = 0.43ms^{-2} $ tonnes | |
| $ T = 35\times10^3 \times 0.43ms^{-2} = 15.2kN $ | |
| $ N + 25 \times 10^{3} = 35 \times 10^{3} \times 0.43ms^{-2} $ | |
| $ N = 9.8kN $ |
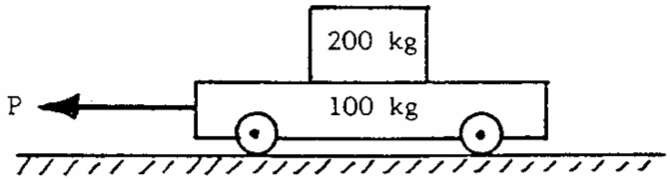
Q7: A 200kg crate rests on a 100kg cart; the coefficient of friction between the crate and cart is 0.25. If the crate is not to slip with respect to the cart, calculate:
a. The maximum allowable magnitude of the force P which may be applied to the cart.
b. The corresponding acceleration of the cart.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ R - mg = m\ddot{y} = 0 $ | |
| $ R = mg $ | |
| $\mu R = m\ddot{x} $ | |
| $ \ddot{x} = 2.45ms^{-2} $ | |
| $ P = M\ddot{x} $ | |
| $ M = 300kg $ | |
| $ P = 735N $ |
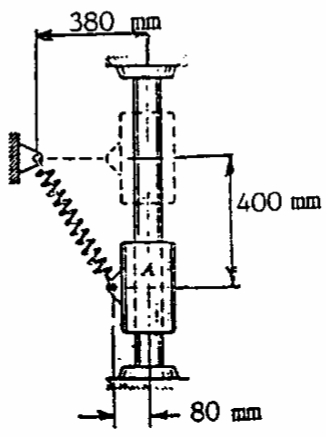
Q8: The collar A has a mass of 10kg and slides on a vertical shaft. The spring is uncompressed when the collar is in the dotted position. Determine the initial acceleration of the collar when it is released from rest in the position illustrated. The coefficient of friction between the collar and the shaft is 0.2, and the stiffness of the spring is $2500Nm^{-1}$
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ T = kx $ | |
| $ R - T\sin \alpha = m\ddot{x} $ | |
| $ R = 300N $ | |
| $ T \cos \alpha - mg - \mu R = m\ddot{y} $ | |
| $ \ddot{y} = 24.2ms^{-1} $ |
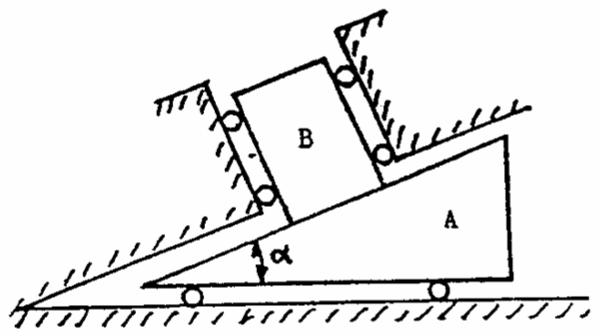
Q9: The wedge A is free to slide without friction on the fixed horizontal surface, and friction may also be negelcted between the plunger B and its guides, which constrain the plunger to slide at right angles to the face of the wedge. Between the plunger and the wedge the coefficient of friction is 0.3. The mass of the wedge is 40kg and that of the plunger 60kg. The system is released from rest. Determine the acceleration of the wedge if the wedge angle is 30 degrees.
Hint: The plunger is accelerating as well as the wedge.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ m_{p}g \cos 30 - R = m_{p}\ddot{x} $ | |
| $ R \sin 30 - \mu R \cos 30 = m_{w}\ddot{y} $ | |
| $ x = y\sin \alpha = y\sin 30 $ | |
| $ \ddot{x}= \ddot{y}\sin \alpha = \ddot{y}\sin 30 $ | |
| $ (m_{p}g\cos30-m_{p}\ddot{x})(\sin30-\mu\cos30) = m_{w}\ddot{y} $ | |
| $ (m_{p}g\cos30-m_{p}\ddot{y}\sin30)(\sin30-\mu\cos30) = m_{w}\ddot{y} $ | |
| $ m_{p}g\cos30(\sin30-\mu\cos30) = m_{w}\ddot{y} + m_{p}\ddot{y}\sin30(\sin30-\mu\cos30) $ | |
| $ \frac{m_{p}g\cos30(\sin30-\mu\cos30)}{m_{w}+m_{p}\sin30(\sin30-\mu\cos30)} = \ddot{y} $ | |
| $ \ddot{x} = 2.59ms^{-2} $ |
Q10: Two bodies of mass 5kg and 20kg slide on 45 degree inclines, as shown, and are connected together by a string which passes over a small, light frictionless pulley at the apex. Motion of the 5kg mass is resisted by a tangential force of 0.2 times the normal reaction (coefficient of friction is 0.2). Motion 20kg mass is resisted by a tangential force which is independent of the normal reaction but varies with sliding velocity according to the relationship:
Tangential force $ = 2.5 \times (Sliding Velocity)^2 $
If the masses are released from rest, calculate the distance they will move before reaching a speed of $4ms^{-1}$
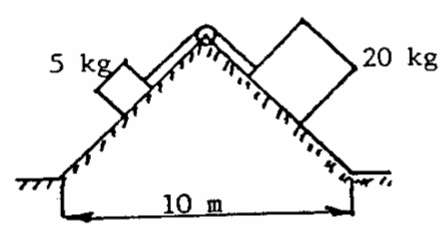
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ R - mg = m\ddot{y} = 0$ | |
| $ R = mg$ | |
| $ T - mg\sin 45 - \mu R = m\ddot{x}$ | |
| $ Mg\sin 45 - T - BV^{2} = M\ddot{x}$ | |
| $ Mg\sin 45 - ( m\ddot{x} + mg\sin 45 + \mu R ) - BV^{2} = M\ddot{x} $ | |
| $ g \sin 45 (M+m) - \mu R - BV^{2} = (M+m) \ddot{x}$ | |
| $ \ddot{x} = 4ms^{-1}$ |
Q11: The power developed by the locomotive of a fast train of total mass 515t is 6MW at the maximum speed of 270km/hr. The rolling resistance os 0.5% of its weight. If the total resistance is of the form $ A + BV^{2} $, calculate the value of B. Calculate also the tractive effort of the locomotive for an initial acceleration of $0.35ms^{-2}$ starting from rest.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ P = Fv $ | |
| $ F = \frac{6 \times 10^{6}}{270/3.6} $ | |
| $ A = BV^{2} $ | |
| $ A = \frac{0.5}{100} \times 515 \times 10^{3} \times 9.81 $ | |
| $ B = 9.73 $ | |
| $ F = ma + A $ | |
| $ F = 515 \times 10^{3} \times 0.35 + 25.3 \times 10^{3} $ |
Q12: The tractive effort of a locomotive of mass 60t is given by:
$T = 125\times 10^{3} $ for $ 0 < v < 75kmhr^{-1}$
$T = \frac{C}{v} $ for $v > 75kmhr^{-1} $
If this train has a maximun speed of 200km/hr on a level straight track, calculate:
a. The maximum acceleration
b. The time taken to reach 175km/hr
c. The distance travelled to reach the same speed
d. The maximum speed up an incline of 1 in 150
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ \ddot{x} = \frac{F - D}{m} $ | |
| $ \ddot{x} = \frac{125\times10^{3}- 4.75\times10^{3}}{300\times10^{3}} $ | |
| $ \ddot{x} = 0.4ms^{-1} $ | |
| $ T = 125 \times 10^{3} = \frac{C}{v} $ | |
| $ C = 2.6 \times 10^{6} $ | |
| $ D = \frac{2.6 \times 10^{6} \times 3.6}{200} $ | |
| $ D = 4.75 + kv^{2} $ | |
| $ k = 13.6 $ | |
| $ \frac{C}{v} - 4.75 \times 10^{3} - BV^{2} = ma $ | |
| $ F = \frac{C}{v} = mg\sin0.38 + 4.75\times 10^{3} + kv^{2} $ |
Q13: The figure shows a small block P of mass 15kg resting on another block Q, of mass 60kg. The small block is held to the rigid wall BC by a rope DE parallel to AB. AB is a plane inclined at an angle of 15 degrees to the horizontal. An external force of 360N parallel to the plane AB acts on the block Q. Draw the Free Body Diagram for each block showing clearly all the forces acting and calculate:
a. The acceleration of Q when the system is released $\ddot{q}$
b. The tension in the rope DE. ($T$)
The coefficient of friction between all surfaces in contact is 0.3.

Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ R - mg\cos15 = m\ddot{y} $ | |
| $ R = 142N $ | |
| $ T - \mu R \sin 15 = m\ddot{x} = 0 $ | |
| $ T = 80.7N $ | |
| $ N - R - mg\cos15 = 0 $ | |
| $ N = 710N $ | |
| $ \mu R + \mu N - 260 - Mg\sin15 = M\ddot{q} $ | |
| $ \ddot{q} = 4.58ms^{-2} $ |