Interactive Online Tutorial Sheets
Tutorial Sheet Five
Q1: A goods wagon of 80 tonne is moving along a horizontal track at 3km/hr in a marshalling yard. A second wagon of 60 tonne, moving at 5km/hr on the same track and in the same direction as the first, reaches it and the two are coupled without rebound by an automatic device. Calculate the common speed of the two coupled wagons and the loss of energy during the coupling operation.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ M_{1}V_{1} + M_{2}V_{2} = 150 \times 10^{3}kgms^{-1} $ | |
| $ (M_{1} + M_{2})V_{final} $ | |
| $ M_{1}V_{1} + M_{2}V_{2} = (M_{1} + M_{2})V_{final} $ | |
| $ V_{final} = 1.07ms^{-1} $ | |
| $ 0.5(M_{1}V_{1}^{2} + M_{2}V_{2}^{2}) $ | |
| $ V_{final} = 1.07ms^{-1} $ |
Q2: The wheels of a car of mass 880kg lock on tarmac $(\mu = 0.9)$ at a speed of $30ms^{-1}$. Estimate the time required to stop.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ F = \mu R = ma $ | |
| $ R = mg $ | |
| $ ma = \mu mg $ | |
| $ a = \mu g $ | |
| $ v = u + at $ | |
| $ -30 = -8.829t $ | |
| $ t = 3.4 $ |
Q3: A 120kg motorbike plus 80kg rider is to accelerate from zero to $5ms^{-1}$ in 0.8s. Estimate the time to stop.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ v = u + at $ | |
| $ 5 = 0 + a(0.8s), a = 6.25 $ | |
| $ F = ma $ | |
| $ F = (120+80)6.25 = 1250 $ |
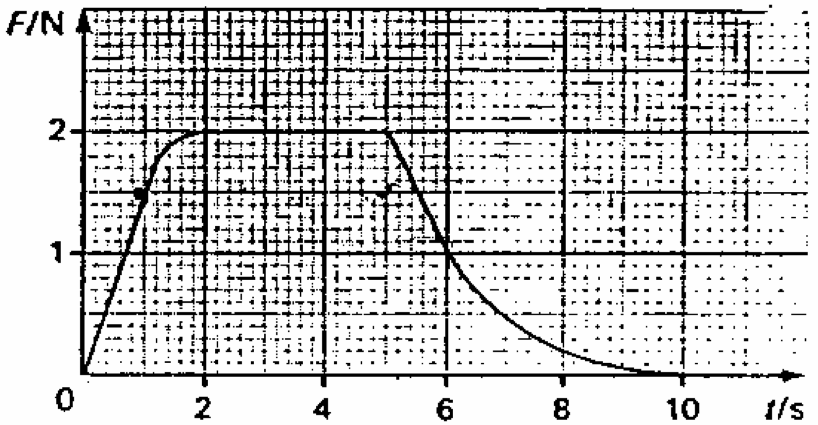
Q4: A very small rocket motor used for controlling a satellite is fired giving a thrust variation shown. Estimate the impulse and, if the satellite mass is 800kg, estimate the speed change.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| Area under the curve = approx $11Ns$ | |
| $ a = \frac{F}{m} = \frac{11}{800}$ |
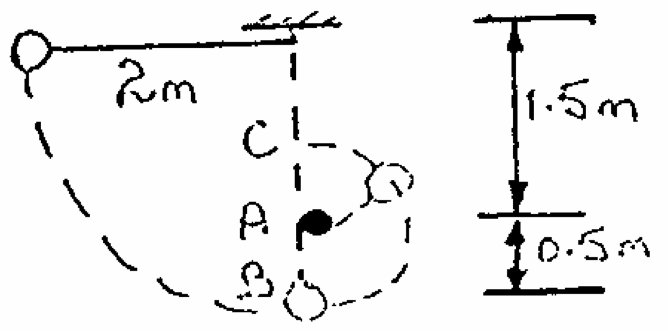
Q5: The weight shown is released from rest with the cord in the horizontal position shown. When the bottom position is reached the cord strikes a small fixed bar a shown and the weight follows the dotted path. Calculate the velocity of the weight at B and C.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ mgh = 2\times9.81\times m = 19.6m $ | |
| $ 0 + \frac{1}{2}mv^2 $ | |
| $ \frac{1}{2}mv^2 = 19.6m, v = 6.26ms^{-1} $ | |
| $ mgh + \frac{1}{2}mv^2 $ | |
| $ 1 \times 9.81 \times m + \frac{1}{2}mv^2 = 19.6m, v = 4.43ms^{-1} $ |
Q6: A buffer has a stiffness given by $K_{1} = 0.25MNm^{-1}$ for compressions up to 200mm and $K_{2}=0.65MNm^{-1}$ for compressions above 200mm. Such a buffer is used to bring to rest a railway truck of 25 tonne moving at $4kmhr^{-1}$. If the rolling resistance is 0.3% of the weight of the truck calculate the compression of the buffer (assuming no rebound).
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ \frac{1}{2}mv^{2} = 15432 $ | |
| $ \frac{1}{2} \times 0.25 \times 0.2^2 + \frac{1}{2} \times 0.65 \times (x-0.2)^2 + 0.25 \times (x-0.2)^2$ | |
| $ \frac{0.3}{100}mgx $ | |
| $ \frac{1}{2}mv^{2} = \frac{1}{2} \times 0.25 \times 0.2^2 + \frac{1}{2} \times 0.65 \times (x-0.2)^2 + 0.25 \times (x-0.2)^2 + \frac{0.3}{100}mgx $ |
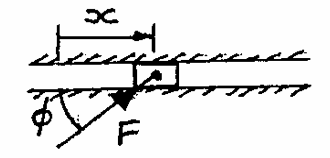
Q7: A force F acts on slider at an angle $\phi$ to the direction of the slide as shown. As the slider moves the force changes in magnitude and direction. If $x$ is the distance moved by the slider.
$F = 60x$ , $\phi=3x^2$
Calculate the word done on the slider by the force F in moving from x=0 to x=0.5m. If the slide is frictionless and the slider is at rest initially calculate the velocity of the slider at x=0.5m. The mass of the slider is 0.8kg.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| Work Done = Force $\times$ Distance | |
| Work Done = $\int60x\cos3x^2\, \mathrm{d}x$ | |
| $x\, \mathrm{d}x = 0.5\int\, \mathrm{d}x^2$ | |
| Work Done = $\int\limits_0^{0.5}30\cos3x^2\, \mathrm{d}x^2$ | |
| $[10\sin3x^2]_0^{0.5} = 6.81J $ | |
| $ \frac{1}{2}mv^{2} = 6.81J, v = 4.12ms^{-1} $ |
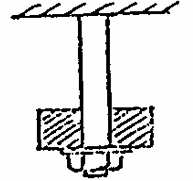
Q7: A solid steel rod 1m long supports a collar of weight 600N as shown. Determine the maximum tension in the rod if the collar, which is free to slide on the rod, is dropped on to the nut from a height of 100mm. The upper end of the rod is rigidly fixed and extension of the rod is proportional to tension, being 0.01mm with a tension of 600N.
Preview: $F = ma$
Click Here for Help with writing the maths
| Working | |
|---|---|
| $ \frac{600}{0.01 \times 10^{-3}} = 60 \times 10^6 Nm^{-1} $ | |
| $ 0.1 \times 600 = 60J $ | |
| $ 60 = \frac{1}{2}kx^{2}, x = 1.41\times10^{-3} $ | |
| $ 60 \times 10^6 \times 1.41 \times 10^{-3} = 84.6kN $ |