Interactive Online Tutorial Sheets
Tutorial Sheet Eight Torsion
| Density ($\rho$) $kg m^{-3}$ |
Young's Modulus ($E$) $GPa$ |
Poisson's Ratio ($v$) | Shear Modulus ($G$) $GPa$ |
Yield Strength $MPa$ |
UTS $MPa$ |
Coeff of lin thm exp ($\alpha$) $10^{-6}K^{-1}$ |
|
|---|---|---|---|---|---|---|---|
| Steel | 7850 | 210 | 0.3 | 80 | 220 | 430 | 11 |
Q1: A solid steel shaft has a diameter of 150 mm and transmits a torque of 50 kNm. Calculate the maximum shear stress in the shaft and the angle of twist over a length of 3m.
| Hints | |
|---|---|
$ J = \frac{\pi}{32}d^4 $ |
|
$ \tau_{max} = \frac{T}{J}\frac{d}{2} $ |
|
$ \theta = \frac{TL}{GJ}$ |
Q2: A hollow steel shaft having an external diameter of 150 mm is to transmit a torque of 26.5 kNm. What should be the internal diameter so that the maximum shear stress is 50 MPa?
| Hints | |
|---|---|
$ r = \frac{Tr}{\tau_{limit}}$ |
|
$ J = \frac{\pi}{32}(d_2^4 - d_1^4)$ |
Q3: A turbo-generator (figure Q3) has an output of 20 MW at $3000 rev min^{−1}$. The efficiency of the generator is 95%. The hollow steel shaft coupling the turbine to the generator has an external diameter of 180 mm and an internal diameter of 100 mm. Determine the maximum shear stress in the shaft.
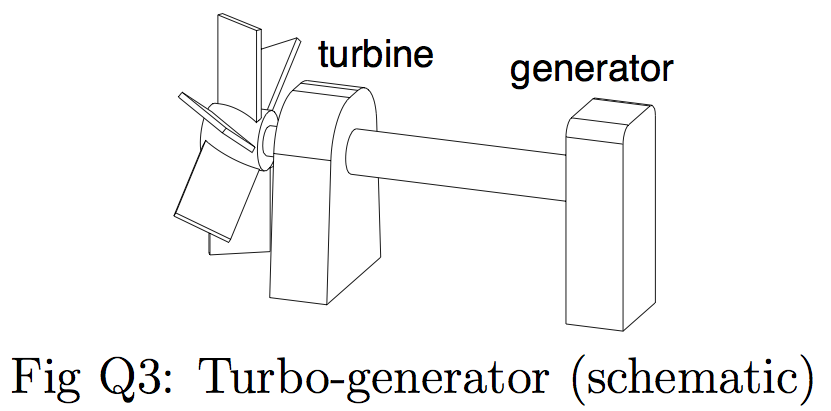
| Hints | |
|---|---|
$\omega$ in $rads^{-1}$ |
|
$ T = \frac{P_t}{\omega} $ |
|
$\tau_{max} = \frac{Td_2}{2J}$ |
Q4: A generator (figure Q4) is driven through a 6 : 1 reduction gear-box by an air turbine which runs at 18000 rev min−1. The turbine develops 40 kW and the gear box losses can be neglected. The generator shaft is hollow and the turbine shaft is solid. Each is 150 mm long and is made of steel for which the maximum working shear stress is limited to 60 MPa. The angle of twist of the generator shaft must not exceed $0.5^{\circ}$. Calculate the inside and outside diameters of the generator shaft and the diameter of the turbine shaft.
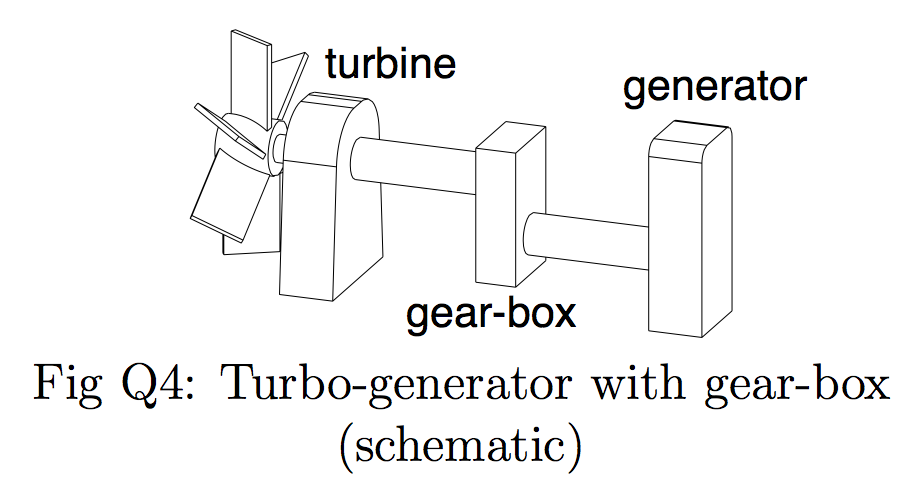
| Hints | |
|---|---|
Calculate the Torque for both the generator and turbine shafts (Note: they will be different) |
|
$J_t = \frac{\pi}{32}d^4_t = \frac{T_td_t}{2\tau_{limit}}$ |
|
$R_g = \frac{\tau_{limit}L}{G\theta_g}$ |
Q5: The stepped steel shaft shown in figure Q5 carries a torque T acting at one end as shown. If the shaft consists of two solid circular sections with the diameters shown, determine the maximum value of $T$ when the (maximum) allowable shear stress is 14 MPa and the rotation of the free end is limited to $3.5^{\circ}$.
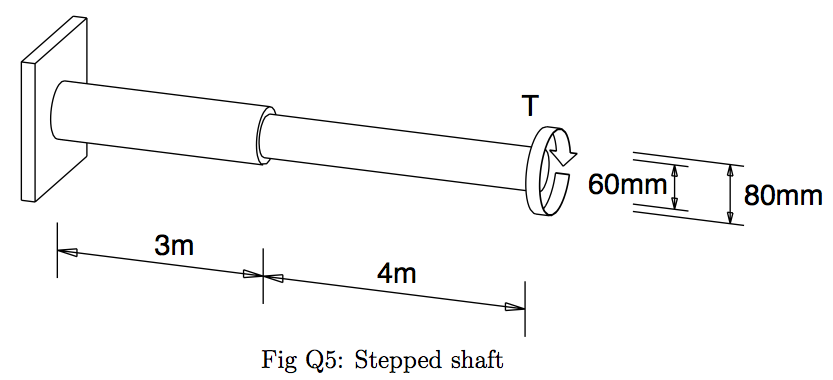
| Hints | |
|---|---|
$ T \leq \frac{2J_1\tau_{limit}}{d_1}$ |
|
$\theta = (\frac{L}{JG})T$ |
|
$\theta_1+\theta_2 = (\frac{L_1}{J_1G}+\frac{L_2}{J_2G})T \leq \frac{3.5\pi}{180}$ |
Q6:
A marine diesel engine which develops 30 kW at $3000 rev min^{−1}$, drives a propeller through a 3 : 1 reduction gearbox. If the efficiency of the gearbox is 85%, determine the minimum diameter of the propeller drive shaft, if the (maximum) allowable shear stress in the material used for the shaft is 70 MPa.
When used to go astern (i.e. in reverse), a 5 : 1 reduction gear is used. Assuming an efficiency of 75% and the same value of (maximum) allowable shear stress as given above, what is the minimum shaft diameter to satisfy both forward and backward conditions?
| Hints | |
|---|---|
Calculate Engine Power, Engine Angular, Prop Power & Propeller Angle Speed |
|
$ \frac{2\tau_{max}}{d_p} = \frac{T_p}{J_p}$ |
|
$d^3_p = \frac{16T_p}{\pi\tau_{max}}$ |